NUMBER THEORY

Consecutive Sum - - - - 2

Divisors          - - - - 8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CONSECUTIVE SUM

•        

•        

•        

 

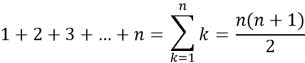
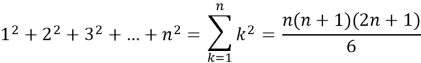
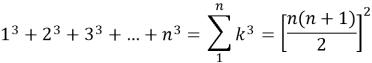
Problem 1

In the following decimal, how many 2’s are there in all before the hundredth 3? (Nigeria, 2008)

Solution

The number of 2’s before the hundredth 3

 

Problem 2

Determine the value of the expression:

1+2-3+4+5-6+7+8-9+10+11-12++94+95-96+97+98-99. (Uganda, 2019)

Solution

1+2-3+4+5-6+7+8-9+10+11-12++94+95-96+97+98-99

=1+2+4+5+7+8++94+95+97+98-3-6-9- -96-99

=1+2+4+5+7+8++94+95+97+98-(3+6+9++96+99)

=1+2+3+4+5+6+7+ +95+96+97+98+99-2(3+6+9+ +96+99)

=1+2+3+4+5+6+7+ +95+96+97+98+99-6(1+2+3++32+33)

 

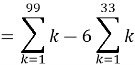
Problem 3

Simplify: 

Solution

 

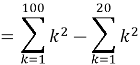
Problem 4

Simplify:

Solution

 

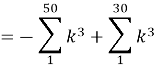
Problem 5

What is

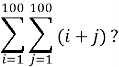
(American Maths Competition, 2018)

Solution

 

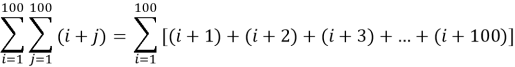
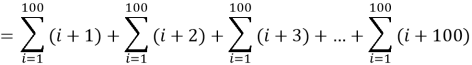
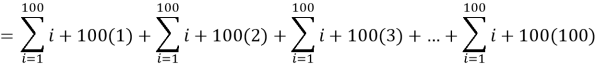
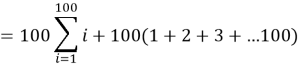
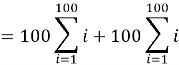
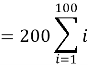
Problem 6

Find the sum of

Solution

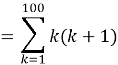
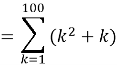
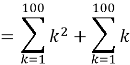
Problem 7

Evaluate as a single fraction. (Uganda, 2017)

Solution

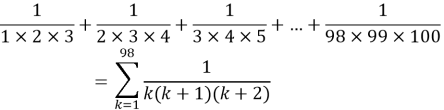
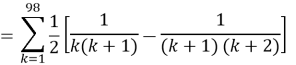
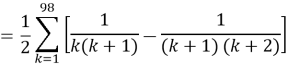
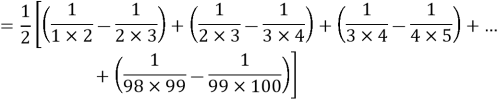
Problem 8

Solution

 

 

 

 

 

 

 

 

 

 

 

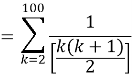
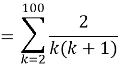
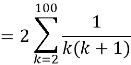
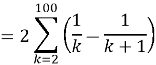
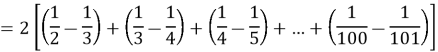
DIVISORS

•         A divisor of a number N is a number that divides N.

•         A divisor of a number yields a reminder of zero upon division.

•         A divisor of a number N is also a factor of the number N.

•         The number of divisors of a number N is denoted as the

•         Given that the prime decomposition of

•         The divisors of 12 are 1,2,3,4,6,12; there are six (6) in number.

•         The divisors of 125 are 1, 5, 25, 125; there are four (4) of them.  

•         Given that P is a prime number,

•         is an odd number if and only if Q is perfect square.

•         The product of all divisors of N is equal to .

•         Given that N is a natural number, .

•         Given is the number of ordered pairs of natural number with

•         The sum of the positive divisors of a natural number N is usually denoted as .

•         Given that the prime decomposition of

•        

•        

•         Given

•        

•         A Natural number N is said to be a perfect number if the sum of its proper divisors is equal to N.

•         A natural number N is a perfect number if the sum of its divisors is equal to twice the number. That is,

•         The four smallest Natural number that are perfect numbers are 6, 28, 496, 8128.

•         Observe the following:

•         Theorem

 

 

Problem 1

Determine the number of ordered pairs of positive integers (a,b) such that the least common multiple of a and b is .

Solution

The required number

 

 

Problem 2

How many positive divisors of is an integer multiple of

Solution

Observe that

Thus, our required answer is the same as the number of positive divisor of

Our required value = 144

 

Problem 3

Determine the product of all distinct natural number divisors of .

Solution

The product of all divisors of N is equal to .

Required product

 

Problem 4

Let How many positive integer divisors of are less than n but do not divide n?

Solution

For every number a, the number of positive divisors less than is equal to the number of divisors greater than

The number of positive divisors of :

The number of positive divisors of less than

The number of positive divisors of n:

The number of proper divisors of n = 9996 – 1= 9995

The number of positive integer divisors of less than n but do not divide n = 19792 – 9995 = 9797

 

Problem 5

In 1984 the engineer and prolific prime-finder Harvey Dubner found the biggest known prime each of whose digits is either a one or a zero. The prime can be expressed as How many digits does this prime have?(Question 25, UK Mathematical Challenge, 2013).

Solution

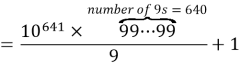
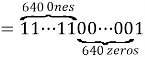
Number of digits of this prime

 

 

Problem 6

Mary chose an even 4-digit number n. she wrote down all the divisors of n in increasing order left to right: 1, 2, …, , n. At some moment Mary wrote 323 as a divisor of n. What is the smallest possible value of the next divisor written to the right of 323? ( Question19, AMC 12B, 2018)

Solution

we are given:

For every two natural number that multiplies to give one is less than the other is greater than

this means the number such that is less than , that is,

Let the divisor written to the right of 323 be  

is right of 323,

Let

 

If 17 and/or 19 are not divisors of then 17 and 19 are divisors of this means (the lcm of 17 and 19). This is a contradiction because we have establish Therefore, 17 and/or 19 are divisors of 

The next multiple of 17 after 323 is 340. the next multiple of 19 after 323 is 342.

Therefore, the smallest value of the next divisor written to the right of 323 is 340.